Senin, 04 Juli 2022
Selasa, 21 Juni 2022
Tigas 14 [Bimo Prasetyo Wibowo] [2103015177] MEMBUAT SOAL DAN JAWABAN
Bimo Prasetyo Wibowo | 2D TI
Nim : 2103015177
MEMBUAT SOAL DAN JAWABAN
Latihan Soal
1. system bilangan yang berbasis 2 dan 16 227(10) dikonversikan ke sistem biner mempunyai nilai
a.11001111
b.11100011 *
c.11110101
d.1110011
2. Bilangan heksadesimal adalah bilangan yang berbasis
a.Bilangan yang berbasis 2 yaitu 0 dan 1
b.Bilangan yang berbasis 16 yaitu 0 dan 17
c.Bilangan yang berbasis 10 yaitu 0 – 9
d.Bilangan yang berbasis 16 yaitu 0 – 9 *
3. urutan bilangan hexadenary C7(16 ) Bilangan Heksadimal dikonversikan ke sistem biner mempunyai nilai
a.11000111(2) *
b.11001111(2)
c.11111000(2)
d.11110001(2)
e.11111101(2)
4. Dasar operasi aritmatika sederhana Operasi logika meliputi perbandingan dua buah elemen logika dengan menggunakan operator logika yaitu kecuali
a. sama dengan (=)
b. tidak sama dengan (<>)
c. lebih besar dari di bagi (>/) *
d. kurang atau sama dengan dari (<=)
5.Ssifat aljabar Boolean asosiatif dari gerbang AND sistem aljabar himpunan atau proposisi yang memenuhi aturan-aturan ekivalen logis merupakan pengertian dari
a.aljabar
b.boolean aljabar
c.aljabar boolean *
d.boolean gerbang AND
6. Sederhanakan K-Map dua variable F = AB + A'B + AB'
a. A+B*
b. B+A
c. A
d. B
7. Sederhanakan K-Map dua variable F = AB' + A'B'
a. A'
b. B' *
c. B
d. A
8. Sederhankan K-Map tiga variable F = ABC' + AB'C' + AB'C + ABC
a. B
b. A'
c. A *
d. B'
9. Sederhanakan K-Map empat variable F = A'BC'D + ABC'D + A'BCD + ABCD
a. BA
b. BC
c. BB
d. BD*
10. Membagi bilangan desimal yang akan diubah, secara berturut – turut dengan pembagian 2, dengan memperhatikan sisa pembagiannya. Merupakan cara konversi bilangan desima ke …
a. Okta
b. Biner *
c. Heksadesimal
d. Bilangan basis 8
Selasa, 14 Juni 2022
"Tugas 13 IMPLEMENTASI COUNTER [BIMO PRASETYO WIBOWO] [2103015177]"
Bimo Prasetyo Wibowo | 2D TI
NIM : 2103015177
IMPLEMENTASI COUNTER
Selasa, 31 Mei 2022
Selasa, 24 Mei 2022
Tugas 9 : Latches, FF, and Timer [Bimo Prasetyo Wibowo] [2103015177]
Bimo Prasetyo Wibowo | 2D TI
NIM : 2103015177
Latches, Flip-Flop and Pewaktu (Timer)
Latches
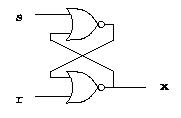
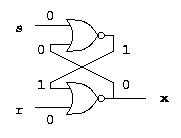
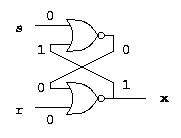
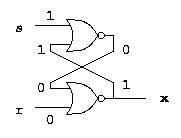
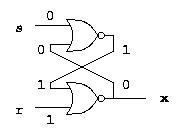 d
d 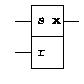
Flip-flops
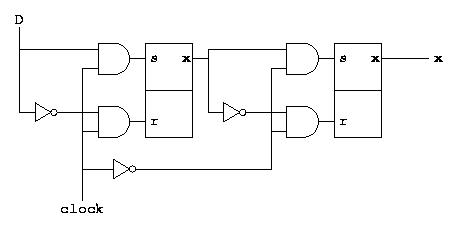
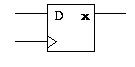
Senin, 09 Mei 2022
Selasa, 26 April 2022
Senin, 18 April 2022
Tugas7 [Bimo Prasetyo Wibowo] Boolean dan Karnaugh Map
Bimo Prasetyo Wibowo | 2D TI
NIM : 2103015177
Mata Kuliah : Sistem Digital dan Gelombang
Aljabar Boolean, Penyederhanaan Logika dan Peta Karnaugh
Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.
Selasa, 12 April 2022
Tugas 6 [Bimo Prasetyo Wibowo] Teorema DeMorgan's
Hukum De Morgan
Untuk membuktikan Persamaan (1-1) perlu di perhatikan, bahwa jikalau semua masukan 1, masing-masing ruas persamaan akan memberikan suatu hasil yang sama dengan 0. Di pihak lain, kalau satu (atau lebih dari satu) masukan sama dengan 0, maka masing-masing ruas persamaan akan memberikan suatu hasil yang sama dengan 1. Sehingga, untuk semua kemungkinan masukan dari ruas sebelah kanan persamaan sama dengan ruas sebelah kiri. Persamaan (1-2) dibuktikan dengan cara yang sama. Hukum De Morgan memperlengkap daftar identitas Boole dasar. Untuk masing-masing acuan selanjutnya, semua hubungan-hubungan tersebut di ringkas dalam tabel 1a.

Diketahui suatu fungsi logika boole EXCLUSIVE OR

dan ekuivalen dengan fungsi logika boole

buktikan bahwa memang kedua persamaan tersebut ekuivalen. Maka dua persamaan tersebut dapat dibuktikan dengan penjabaran dengan pertolongan aljabar boole sebagai berikut:








 menggambarkan terminal keluaran yang sama, A dan menggambarkan terminal masukan yang sama, dan lain sebagainya. Rangkaian yang melaksanakan logika AND positif dalam persamaan (1-3) juga bekerja sebagai gerbang logika OR negatif pada persamaan (1-4). Alasan yang sama digunakan untuk membuktikan, bahwa rangkaian yang sama mungkin berlaku sebagai AND negatif atau OR positif, tergantung kepada bagaimana tingkat biner didefinisikan. Hal ini telah dibuktikan untuk logika dioda. Untuk lebih jelasnya berikut ditampilkan aplikasi teorema De Morgan dalam diagram blok fungsi logika boole pada gambar 1-1c. Suatu OR yang diubah ke AND dengan membalikkan semua masukan dan keluarannya, gambar 1-1d. Suatu AND menjadi OR, kalau semua masukan dan keluaran komplemen.
menggambarkan terminal keluaran yang sama, A dan menggambarkan terminal masukan yang sama, dan lain sebagainya. Rangkaian yang melaksanakan logika AND positif dalam persamaan (1-3) juga bekerja sebagai gerbang logika OR negatif pada persamaan (1-4). Alasan yang sama digunakan untuk membuktikan, bahwa rangkaian yang sama mungkin berlaku sebagai AND negatif atau OR positif, tergantung kepada bagaimana tingkat biner didefinisikan. Hal ini telah dibuktikan untuk logika dioda. Untuk lebih jelasnya berikut ditampilkan aplikasi teorema De Morgan dalam diagram blok fungsi logika boole pada gambar 1-1c. Suatu OR yang diubah ke AND dengan membalikkan semua masukan dan keluarannya, gambar 1-1d. Suatu AND menjadi OR, kalau semua masukan dan keluaran komplemen.

Sekarang jelas bahwa sebenarnya tidak perlu menggunakan semua gerbang logika, yakni cukup adanya OR dan NOT atau AND dan NOT saja, karena dari hukum De Morgan persamaan (1-1) AND dapat diperoleh dari OR dan NOT, seperti ditunjukkan dalam gambar 1-1c. Dan dengan cara yang sama, AND dan NOT dapat dipilih sebagai rangkaian gerbang logika dasar, dan dari hukum De Morgan persamaan (1-2), OR mungkin dapat dibangun seperti ditunjukkan dalam gambar 1-1d. Gambar ini akan menjelaskan lagi, bahwa OR (AND) dibalikkan pada masukan dan keluaran membentuk logika AND (OR)
Senin, 04 April 2022
Tugas 5 [Bimo Prasetyo Wibowo] Aljabar Boolean
Bimo Prasetyo Wibowo | 2D TI
NIM : 2103015177
Mata Kuliah : Sistem Digital dan Gelombang
Aturan - aturan Aljabar Boolean
Pengertian
Hukum Aljabar Boolean
Hukum Komutatif (Commutative Law)
Hukum Komutatif menyatakan bahwa penukaran urutan variabel atau sinyal Input tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
X.Y = Y.X
Penjumlahan (Gerbang Logika OR)
X+Y = Y+X
Catatan : Pada penjumlahan dan perkalian, kita dapat menukarkan posisi variabel atau dalam hal ini adalah sinyal Input, hasilnya akan tetap sama atau tidak akan mengubah keluarannya.
Hukum Asosiatif (Associative Law)
Hukum Asosiatif menyatakan bahwa urutan operasi logika tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
W . (X . Y) = (W . X) . Y
Penjumlahan (Gerbang Logika OR)
W + (X + Y) = (W + X) + Y
Catatan : Pada penjumlahan dan perkalian, kita dapat mengelompokan posisi variabel dalam hal ini adalah urutan operasi logikanya, hasilnya akan tetap sama atau tidak akan mengubah keluarannya. Tidak peduli yang mana dihitung terlebih dahulu, hasilnya tetap akan sama. Tanda kurung hanya sekedar untuk mempermudah mengingat yang mana akan dihitung terlebih dahulu.
Hukum Distributif
Hukum Distributif menyatakan bahwa variabel-variabel atau sinyal Input dapat disebarkan tempatnya atau diubah urutan sinyalnya, perubahan tersebut tidak akan mempengaruhi Output Keluarannya.
Hukum AND (AND Law)
Disebut dengan Hukum AND karena pada hukum ini menggunakan Operasi Logika AND atau perkalian. Berikut ini contohnya :
Hukum OR (OR Law)
Hukum OR menggunakn Operasi Logika OR atau Penjumlahan. Berikut ini adalah Contohnya :
Hukum Inversi (Inversion Law)
Hukum Inversi menggunakan Operasi Logika NOT. Hukum Inversi ini menyatakan jika terjadi Inversi ganda (kebalikan 2 kali) maka hasilnya akan kembali ke nilai aslinya.
Jadi, jika suatu Input (masukan) diinversi (dibalik) maka hasilnya akan berlawanan. Namun jika diinversi sekali lagi, hasilnya akan kembali ke semula.
Prioritas Operasi Aljabar Boolean
Selasa, 29 Maret 2022
Tugas 4 [Bimo Prasetyo Wibowo] Gerbang Logika
Bimo Prasetyo Wibowo | 2D TI
NIM : 2103015177
Mata Kuliah : Sistem Digital dan Gelombang
Gerbang Logika dan Aljabar Boolean
A. PENGERTIAN
B. Jenis-jenis Gerbang Logika Dasar dan Simbolnya
Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :
- Gerbang AND
- Gerbang OR
- Gerbang NOT
- Gerbang NAND
- Gerbang NOR
- Gerbang X-OR (Exclusive OR)
- Gerbang X-NOR (Exlusive NOR)
- HIGH (tinggi) dan LOW (rendah)
- TRUE (benar) dan FALSE (salah)
- ON (Hidup) dan OFF (Mati)
- 1 dan 0
Gerbang AND (AND Gate)
Gerbang OR (OR Gate)
Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0.
Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.
Simbol dan Tabel Kebenaran Gerbang OR (OR Gate)





















